---
title: 5 Python Modules for Scientific Computing
description: Explore 5 essential Python modules for scientific computing, from NumPy for numerical calculations to VPython for 3D visualization. Enhance your coding skills today!
image: https://blog.rheinwerk-computing.com/hubfs/5%20Python%20Modules%20for%20Scientific%20Computing.png
---
[](https://blog.rheinwerk-computing.com/) [Blog](https://blog.rheinwerk-computing.com)
- Books
- Get an overview of our wide selection of books on every relevant computing topic.
- [General Computing](https://www.sap-press.com/rheinwerk-computing/general-computing/)
- [DevOps](https://www.sap-press.com/rheinwerk-computing/devops/)
- [Programming Languages](https://www.sap-press.com/rheinwerk-computing/programming-languages/)
- [Security](https://www.sap-press.com/rheinwerk-computing/security/)
- [Software Development](https://www.sap-press.com/rheinwerk-computing/software-development/)
- Book Subscription
- Get unlimited access to all Rheinwerk Computing books!
- [Programming Subscription](https://sap-press.com/subscriptions/)
[Python](https://blog.rheinwerk-computing.com/tag/python)
# 5 Python Modules for Scientific Computing
 by [Rheinwerk Computing](https://blog.rheinwerk-computing.com/author/rheinwerk-computing)
Let’s take a look at the capabilities and features of the module concept in Python; we’ll describe five scientific computing modules in a keyword-like manner.
Instead of *module*, the terms *library* or *software library* are also commonly used. The capabilities of [Python](https://learning.rheinwerk-computing.com/python)are best illustrated by using short sample programs. Of course, you don’t need understand the source code shown in this blog post. This is just to introduce you to the different modules.
## NumPy
The NumPy module (**num**erical **Py**thon) enables you to perform extensive numerical calculations. For example, you can solve linear systems of equations, even with complex numbers. Below shows a simple vector calculus program.
`01 import numpy as np`
`02 A=np.array([1, 2, 3])`
`03 B=np.array([4, 5, 6])`
`04 print("Vector A:",A)`
`05 print("Vector B:",B)`
`06 print("Total A+B:",A+B)`
`07 print("Product A*B:",A*B)`
`08 print("Cross product :",np.cross(A,B))`
`09 print("Scalar product:",np.dot(A,B))`
**Output**
Vector A: \[1 2 3\]
Vector B: \[4 5 6\]
Total A+B: \[5 7 9\]
Product A\*B: \[ 4 10 18\]
Cross product : \[-3 6 -3\]
Scalar product: 32
## Matplotlib
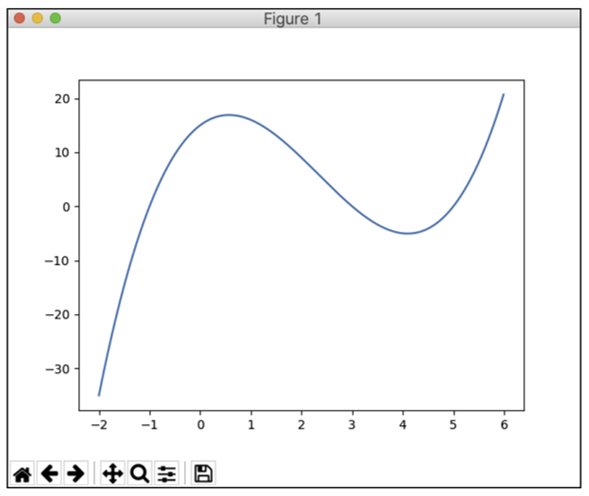
The Matplotlib module allows you to display mathematical functions, histograms, and many other diagram types as well as to simulate and animate physical processes. The graphical design options are remarkably diverse and rich in detail. Below shows a simple example of the function plot of a polynomial.
`01 import numpy as np`
`02 import matplotlib.pyplot as plt`
`03 x=np.arange(-2,6,0.01)`
`04 y=x**3-7*x**2+7*x+15`
`05 plt.plot(x,y)`
`06 plt.show()`
**Output**
This figure shows the output of the function plot.
## SymPy
Using SymPy (**sym**bolic **Py**thon), you can calculate integrals or derivatives symbolically or solve differential equations symbolically. A simplification of mathematical terms is also possible (and much more). The code below shows a simple example of symbolic differentiation and integration.
`01 from sympy import *`
`02 x=symbols("x")`
`03 y=x**3-7*x**2+7*x+15`
`04 y_1=diff(y,x,1)`
`05 y_2=diff(y,x,2)`
`06 y_3=diff(y,x,3)`
`07 Y=integrate(y,x)`
`08 print("1. Derivative:",y_1)`
`09 print("2. Derivative:",y_2)`
`10 print("3. Derivative:",y_3)`
`11 print(" Integral :",Y)`
**Output**
1. Derivative: 3\*x\*\*2 - 14\*x + 7
2. Derivative: 2\*(3\*x - 7)
3. Derivative: 6
Integral : x\*\*4/4 - 7\*x\*\*3/3 + 7\*x\*\*2/2 + 15\*x
## SciPy
SciPy (**sci**entific **Py**thon) allows you to numerically differentiate, integrate, and numerically solve systems of differential equations. SciPy is as comprehensive as it is versatile. The capabilities of SciPy can only be partially described in this book. Below is a simple example of a numerical integration program.
`01 import scipy.integrate as integral`
`02 def f(x):`
`03 return x**2`
`04 A=integral.quad(f,0,5)`
`05 print("Area A=",A[0])`
**Output**
Area A= 41.66666666666666
## VPython
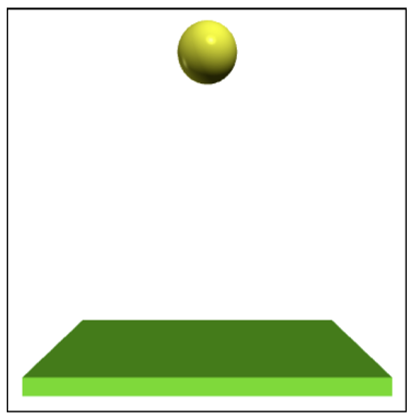
Using VPython, you can display fields in a 3D view or even animate their movements in 3D space. As of version 7, the animations are displayed in the standard browser after the program starts. The final listing shows an example of how you can program the animation of a bouncing ball.
`01 from vpython import *`
`02 r=1. #radius`
`03 h=5. #height`
`04 scene.background=color.white`
`05 scene.center=vector(0,h,0)`
`06 box(pos=vector(0,0,0),size=vector(2*h,r/2,h), color=color.green)`
`07 ball = sphere(radius=r, color=color.yellow)`
`08 ball.pos=vector(0,2*h,0) #drop height`
`09 ball.v = vector(0,0,0) #initial velocity`
`10 g=9.81`
`11 dt = 0.01`
`12 while True:`
`13 rate(100)`
`14 ball.pos = ball.pos + ball.v*dt`
`15 if ball.pos.y < r:`
`16 ball.v.y = -ball.v.y`
`17 else:`
`18 ball.v.y = ball.v.y - g*dt`
**Output**
The figure below shows a snapshot of the animation.
Editor’s note: This post has been adapted from a section of the book *[Python for Engineering and Scientific Computing](https://www.sap-press.com/python-for-engineering-and-scientific-computing_5852/?utm_source=sappressblog&utm_medium=referral&utm_campaign=Blogs&utm_term=2559_chapter1&utm_content=2559)* by Veit Steinkamp. Dr. Steinkamp studied electrical engineering and German to become a teacher and pass on his knowledge at vocational schools and technical colleges. He teaches electrical engineering, application development, and mechanical engineering technology. He has also taught theoretical electrical engineering and the fundamentals of electrical engineering.
This post was originally published 4/2024.
## Recommendation
[](https://www.sap-press.com/python-for-engineering-and-scientific-computing_5852/?utm_source=sappressblog&utm_medium=referral&utm_campaign=Blogs&utm_term=2559_chapter1&utm_content=2559)
**Python for Engineering and Scientific Computing**
It’s finally here—your guide to Python for engineers and scientists, by an engineer and scientist! Get to know your development environments and the key Python modules you’ll need: NumPy, SymPy, SciPy, Matplotlib, and VPython. Understand basic Python program structures and walk through practical exercises that start simple and increase in complexity as you work your way through the book. With information on statistical calculations, Boolean algebra, and interactive programming with Tkinter, this Python guide belongs on every scientist’s shelf!
[Learn More](https://www.sap-press.com/python-for-engineering-and-scientific-computing_5852/?utm_source=sappressblog&utm_medium=referral&utm_campaign=Blogs&utm_term=2559_chapter1&utm_content=2559)
**by [Rheinwerk Computing](https://blog.rheinwerk-computing.com/author/rheinwerk-computing)**
Rheinwerk Computing is an imprint of Rheinwerk Publishing and publishes books by leading experts in the fields of programming, administration, security, analytics, and more.
[Python](https://blog.rheinwerk-computing.com/tag/python) [Programming Languages](https://blog.rheinwerk-computing.com/tag/programming-languages)
[](https://www.facebook.com/share.php?u=https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Dfacebook) [](https://www.linkedin.com/shareArticle?mini=true&url=https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Dlinkedin) [](https://twitter.com/intent/tweet?original_referer=https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Dtwitter&url=https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Dtwitter&source=tweetbutton&text=) [](mailto:?subject=Check+out+https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Demail&body=Check+out+https%3A%2F%2Fblog.rheinwerk-computing.com%2F5-python-modules-for-scientific-computing%3Futm_medium%3Dsocial%26utm_source%3Demail)
### Comments
### Latest Blog Posts
[](https://blog.rheinwerk-computing.com/how-to-create-your-first-python-program)
[Python](https://blog.rheinwerk-computing.com/tag/python)
## [How to Create Your First Python Program](https://blog.rheinwerk-computing.com/how-to-create-your-first-python-program)
[Read More](https://blog.rheinwerk-computing.com/how-to-create-your-first-python-program)
[](https://blog.rheinwerk-computing.com/how-to-use-python-to-randomly-generate-numbers)
[Python](https://blog.rheinwerk-computing.com/tag/python)
## [How to Use Python to Randomly Generate Numbers](https://blog.rheinwerk-computing.com/how-to-use-python-to-randomly-generate-numbers)
[Read More](https://blog.rheinwerk-computing.com/how-to-use-python-to-randomly-generate-numbers)
**Subscribe to our blog!**Get notified about future blog updates.
-
-
-
### The official Rheinwerk Computing Blog
Rheinwerk Computing is an imprint of Rheinwerk Publishing and publishes resources that will help you accelerate your computing journey. The Rheinwerk Computing Blog is designed to provide helpful, actionable information on a variety of topics, including programming, administration, security, and analytics!
### Blog Topics
- [All Topics](https://blog.rheinwerk-computing.com)
- [Programming Languages](https://blog.rheinwerk-computing.com/tag/programming-languages)
- [How To](https://blog.rheinwerk-computing.com/tag/how-to)
- [JavaScript](https://blog.rheinwerk-computing.com/tag/javascript)
- [DevOps](https://blog.rheinwerk-computing.com/tag/devops)
- [Web Development](https://blog.rheinwerk-computing.com/tag/web-development)
- [Python](https://blog.rheinwerk-computing.com/tag/python)
- [What Is?](https://blog.rheinwerk-computing.com/tag/what-is)
- [Cybersecurity](https://blog.rheinwerk-computing.com/tag/cybersecurity)
- [Software Development](https://blog.rheinwerk-computing.com/tag/software-development)
- [Java](https://blog.rheinwerk-computing.com/tag/java)
### Blog curated by
[](https://www.sap-press.com/rheinwerk-computing/) [Visit Rheinwerk Computing Store](https://www.sap-press.com/rheinwerk-computing/)
### About
- [Home](https://sap-press.com/)
- [About Us](https://sap-press.com/the-publisher/)
- [Contact](mailto:info@rheinwerk-publishing.com)
- [Legal Notes](https://sap-press.com/legal-notes/)
- [Privacy Policy](https://sap-press.com/privacy/)
- [Terms of Use](https://sap-press.com/terms/)
© 2026 Rheinwerk Publishing, Inc. | Change Privacy Options
```json
{
"@context" : "https://schema.org",
"@type" : "BlogPosting",
"author" : {
"@type" : "Person",
"name" : "Rheinwerk Computing",
"url" : "https://blog.rheinwerk-computing.com/author/rheinwerk-computing"
},
"dateModified" : "2025-04-30T12:02:55.367Z",
"datePublished" : "2024-04-05T13:10:00.000Z",
"headline" : "5 Python Modules for Scientific Computing",
"image" : [ "https://blog.rheinwerk-computing.com/hubfs/5%20Python%20Modules%20for%20Scientific%20Computing.png" ],
"mainEntityOfPage" : {
"@id" : "https://blog.rheinwerk-computing.com/5-python-modules-for-scientific-computing",
"@type" : "WebPage"
},
"publisher" : {
"@type" : "Organization",
"logo" : {
"@type" : "ImageObject",
"url" : "https://blog.rheinwerk-computing.com/hubfs/Logo-1.jpg"
},
"name" : "Rheinwerk Publishing, Inc."
}
}
```